Oscilator mecanic liber cu frecare. Amortizarea

Experienţa arată că toţi oscilatorii mecanici liberi efectuează oscilaţii a căror amplitudine scade �n timp, numite oscilaţii amortizate. Cauza este scăderea energiei mecanice a oscilatorului datorată frecărilor cu mediul �n care sistemul oscilează:

Energia mecanică este transferată parţial mediului sub formă de căldură şi parţial sistemului �nsuşi ca energie internă. Scăderea progresivă a energiei mecanice duce la scăderea amplitudinii. Un oscilator neamortizat este un caz ideal.

Se disting două tipuri de amortizare, după cum forţele de frecare sunt datorate unui fluid (gaz, lichid) sau unui solid �n contact cu oscilatorul.

Amortizarea fluidă

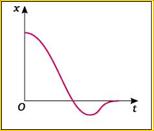
�n figura alăturata este reprezentat un dispozitiv experimental destinat observării variaţiilor

amplitudinii oscilatorului cu frecare v�scoasă. Paleta ataşată oscilatorului este introdusă �ntr-un lichid.

�n felul acesta, oscilatorul �nt�mpină la �naintare o forţă de rezistenţă pe care o putem considera proporţională cu viteza lui:

            (1)

Aceasta este responsabilă, �n cea mai mare parte, de amortizarea oscilaţiilor.

 Constanta C, măsurată �n N∙s/m, depinde de v�scozitatea fluidului şi de aria secţiunii transversale a corpului �n contact cu fluidul. Dacă paleta este cufundată mai ad�nc �n fluid, amortizarea este mai rapidă.

Cu ajutorul unui calculator cu interfaţă (sau a unui osciloscop) se poate vizualiza şi �nregistra variaţia �n timp a oscilaţiei amortizate.  

Curba obţinută reprezintă variaţia �n timp a elongaţiei sistemului. Aceasta nu mai este o sinusoidă, căci amplitudinea scade progresiv.

Totuşi, valorile maxime ale elongaţiei sunt atinse la intervale de timp succesive egale.

Mişcarea oscilatorie amortizată este numită pseudoperiodică, iar T, pseudoperioada acesteia. Pseudoperioada T este puţin mai mare dec�t perioada proprie T₀ a oscilatorului fără frecări:

                                          T > T₀  (2)

şi creşte o dată cu creşterea coeficientului de frecare fluidă C.

 Principiul fundamental al dinamicii aplicat, de exemplu, unui oscilator elastic cu frecare fluidă, scris sub forma

�n proiecţie pe direcţia de oscilaţie, devine:

Cum reprezintă pătratul pulsaţiei proprii �n absenţa frecărilor, se obţine ecuaţia:

Se demonstrează că pentru  , soluţia ecuaţiei reprezintă legea unei mişcări oscilatorii de forma:

 Amplitudinea oscilaţiei: scade exponenţial cu timpul şi această scădere este cu at�t mai accentuată cu c�t coeficientul C de frecare v�scoasă este mai mare. Reprezentarea grafică a legii de mişcare este redată �n figura alăturată.

Dacă frecarea devine importantă (), oscilatorul, o dată scos din poziţia de echilibru, revine �n această poziţie fără a mai oscila: mişcarea se numeşte aperiodică

Pentru , amortizarea este numită critică.

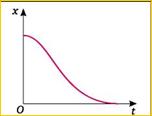
 Amortizarea uscată

Amplitudinea mişcării unui oscilator elastic orizontal aflat �n contact permanent cu o suprafaţă plană, cu frecare mică, scade liniar �n timp  p�nă la oprirea definitivă a mobilului. Dacă frecarea este mare, mobilul revine �n poziţia de echilibru cu viteză nulă şi nu mai oscilează.